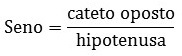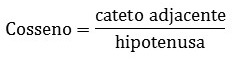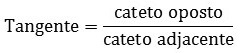Entendendo a Matemática

A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos. Ela é utilizada também em outras áreas de estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.
Funções Trigonométricas
As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.
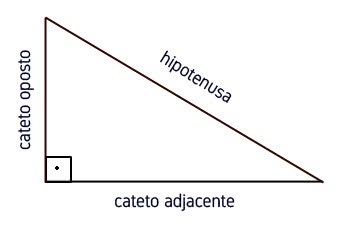
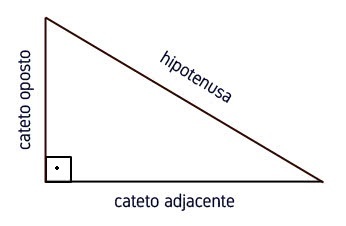
As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo. Elas são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
Teorema de Pitágoras
O Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. – 495 a.C.), é muito utilizado nos estudos trigonométricos.
Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:
a2 = b2 + c2
Sendo, a: hipotenusa; c e e: catetos
No Enem, contamos como questão certa essa parte da matéria. Algumas aplicações envolvendo triângulos retângulos para você observar.
Exercício 1
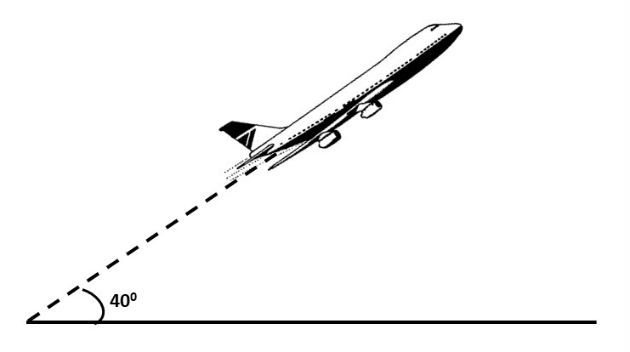
A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?
Considere:
sen 40º = 0,64
cos 40º = 0,77
tg 40º = 0,84
Solução
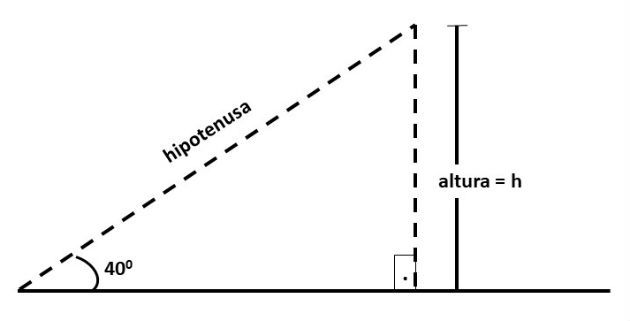
Vamos começar o exercício representando na figura a altura do avião. Para isso, basta desenhar uma reta perpendicular à superfície e que passa pelo ponto onde o avião se encontra.
Notamos que o triângulo indicado é retângulo e a distância percorrida representa a medida da hipotenusa deste triângulo e a altura do cateto oposto ao ângulo dado.
Portanto, usaremos o seno do ângulo para encontrar a medida da altura:
Assim, ao percorrer 8 000 m, o avião se encontra a 5 120 m de altura.
Exercício 2
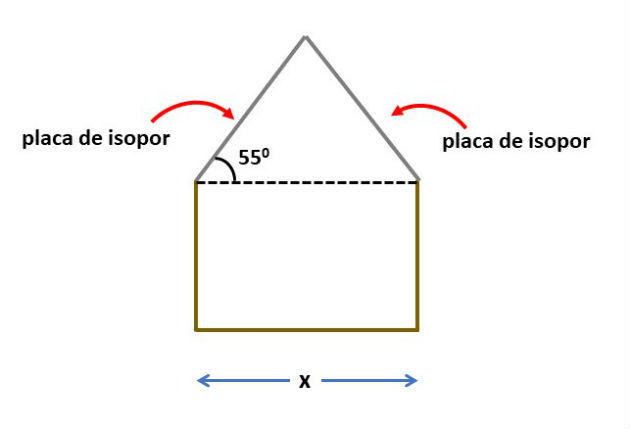
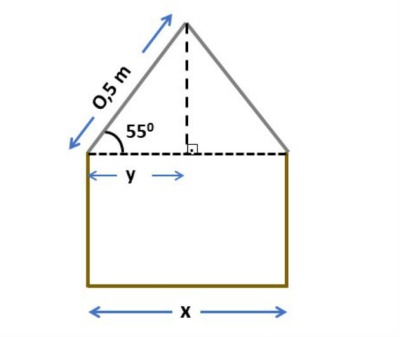
Para uma feira de ciências um grupo de estudantes resolveu construir uma maquete de uma casa, conforme esquema abaixo. O telhado será feito com uma placa de isopor de 1m de comprimento, que será dividida ao meio para fazer as duas partes do telhado. Sabendo que o telhado será feito segundo um ângulo de 55º, calcule a medida x da largura casa.
Considere:
sen 55º = 0,82
cos 55º = 0,57
tg 55º = 1,43
Solução
Como o telhado da maquete será feito com uma placa de isopor de 1m de comprimento, ao dividir a placa ao meio, a medida de cada lado do telhado será igual a 0,5 m.
O ângulo de 55º é o ângulo formado entre a reta que representa o telhado e uma reta na direção horizontal. Se unirmos essas retas, formamos um triângulo isósceles (dois lados de mesma medida).
Vamos então traçar a altura deste triângulo. Como o triângulo é isósceles, essa altura divide a sua base em segmentos de mesma medida que chamamos de y, conforme figura abaixo:
A medida y será igual a metade da medida de x, que corresponde a largura da casa.
Desta forma, temos a medida da hipotenusa do triângulo retângulo e procuramos a medida de y, que é o cateto adjacente ao ângulo dado.
Assim, podemos usar o cosseno de 55º para calcular esse valor:
Como a largura da casa é igual a duas vezes essa medida, então temos:
largura da casa = 2. 0,285 = 0,57
Assim, a maquete da casa terá uma largura de 0,57 m ou 57 cm.
Exercício 3
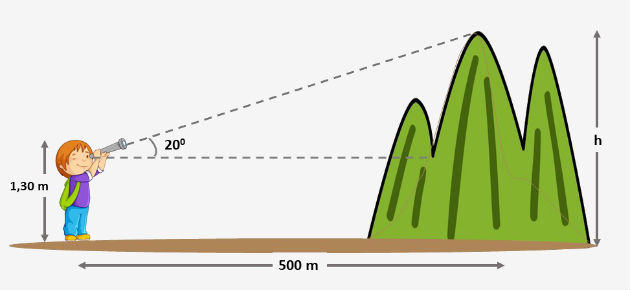
Um menino avista o ponto mais alto de um morro, conforme figura abaixo. Considerando que ele está a uma distância de 500 m da base do morro, calcule a altura (h) deste ponto.
Considere:
sen 20º = 0,34
cos 20º = 0,93
tg 20º = 0,36
Solução
Observando o desenho, notamos que o ângulo visual é de 20º. Para calcular a altura do morro, iremos usar as relações do seguinte triângulo:
Como o triângulo é retângulo, iremos calcular a medida x usando a razão trigonométrica tangente.
Escolhemos essa razão, visto que conhecemos o valor do ângulo do cateto adjacente e estamos procurando a medida do cateto oposto (x).
Assim, teremos:
Como o menino tem 1,30 m, a altura do morro será encontrada somando-se este valor ao valor encontrado para x. Assim, teremos:
h = 180 + 1,3 =181,3
Logo, a altura do morro será igual a 181,3 m.